Symmetry in Equations

Equations can have symmetry:

x^2
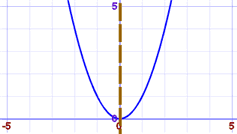
Graph of xtwo
Symmetry about y-axis

x^2
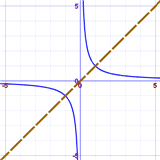
Graph of ane/ten
Diagonal symmetry

In other words, in that location is a mirror-prototype.

Benefits

The benefits of finding symmetry in an equation are:

  • we understand the equation better
  • it is easier to plot
  • it can be easier to solve. When nosotros find a solution on 1 side, nosotros can then say "likewise, by symmetry, the (mirrored value)"

How to Check For Symmetry

We can often see symmetry visually, but to be really sure we should check a elementary fact:

Is the equation unchanged when using symmetric values?

How we exercise this depends on the blazon of symmetry:

For Symmetry Virtually Y-Axis

For symmetry with respect to the Y-Axis, check to see if the equation is the same when we replace x with −x:

For Symmetry About Ten-Centrality

Use the same thought as for the Y-Axis, but endeavour replacing y with −y.

Instance: is y = x3 symmetric well-nigh the ten-centrality?

Endeavor to replace y with −y:

−y = xiii

At present try to become the original equation:

Try multiplying both sides by −ane:

y = −xthree

Information technology is dissimilar.

Then y = x3 is not symmetric most the y-axis

Diagonal Symmetry

Endeavour swapping y and x (i.e. replace both y with 10 and x with y).

Instance: does y = 1/ten have Diagonal Symmetry?

Start with:

y = 1/x

Endeavour swapping y with ten:

ten = one/y

Now rearrange that: multiply both sides by y:

xy = ane

And then divide both sides by 10:

y = one/x

And we have the original equation. They are the same.

So y = ane/ten has Diagonal Symmetry

Origin Symmetry

origin symmetry

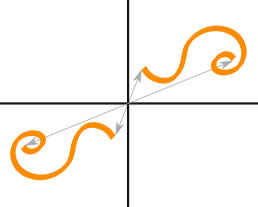
Origin Symmetry is when every part has a matching part:

  • the same altitude from the primal signal
  • but in the contrary direction.

Cheque to come across if the equation is the same when we replace both 10 with −x and y with −y.

Example: does y = 1/ten have Origin Symmetry?

Showtime with:

y = 1/x

Replace x with −x and y with −y:

(−y) = 1/(−x)

Multiply both sides by −ane:

y = 1/x

And we have the original equation.

So y = i/x has Origin Symmetry

Amazing! y = 1/ten has origin symmetry likewise as diagonal symmetry!

1154, 1155, 2463, 2464, 2465, 4042, 4043, 4044, 4045, 4046